2차원 배열을 사용한 풀이
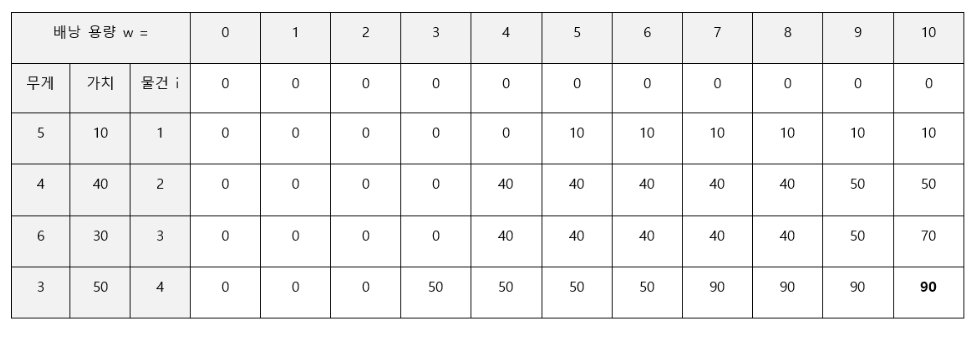
각 물건마다 배낭 용량을 늘려가며
- '이거 넣어질까?' (= 물건을 넣을만큼 배낭 용량이 충분한가?)
- '넣었을 때, 안 넣은 경우보다 가치가 높은가?'
이 2가지를 물어보면 끝이다.
물건 1의 무게는 5이므로 배낭 용량 5 이상부터 1개 넣을 수 있다. 당장은 비교할 최댓값 없으니 다 넣는다.
물건 2의 무게는 4이므로 배낭 용량 4 이상부터 1개를 넣을까 말까 고민해야 한다.
배낭 용량 4일 때는 비교할 최댓값이 없었으니 그냥 넣는다.
배낭 용량 5일 때 물건 2를 1개 넣어봤더니 가치가 40이다. 이전의 최대 가치보다 크므로 채택한다.
... 같은 방식으로 진행한다.
물건 3의 무게는 6이므로 배낭 용량 6 이상부터 1개 넣을까 말까 고민해야 한다.
배낭 용량 6일 때 물건 3을 1개 넣어봤더니 가치가 30이다. 이전의 최대 가치가 더 크므로 채택하지 않는다.
...
배낭 용량 10일 때 물건 3을 1개 넣어봤더니 남은 배낭 용량이 4이다.
배낭 용량 4에 대한 최댓값(3은 넣으면 안됨)은 40이다. 이것과 물건 3의 가치를 더하면 70이다.
이전의 최대 가치인 50과 비교하면 더 크므로 채택한다.
이거 반복하면 맨 마지막 칸에 최대 가치 구할 수 있음.
모든 배낭 용량에 대해 모든 물건의 최적의 경우의 수를 구할 수 있기 때문이다.
1차원 배열을 사용한 풀이
import sys
input = sys.stdin.readline
# N = 물품의 수, K = 배낭 용량
N, K = map(int, input().split())
objs = [tuple(map(int, input().split())) for _ in range(N)]
# dp[i]는 i 무게에서의 최대 가치를 저장합니다
dp = [0] * (K + 1)
# 각 물건의 무게와 가치를 가져옵니다
for weight, value in objs:
# 역순으로 순회하여 중복 사용을 방지합니다
for j in range(K, weight - 1, -1):
dp[j] = max(dp[j], dp[j - weight] + value)
print(dp[K])
각 물건에 대해 순회를 하고 이제까지 구한 최적의 가치와 비교하는 것은
2차원 배열을 사용할 때와 동일하다.
하지만 최적의 물건 가치를 매번 같은 배열에 저장하므로
역으로 순회하여 중복(같은 물건을 2번 넣는 일)이 발생하지 않도록 한다.
역으로 순회한다는게 처음 보면 이해가 안될수도 있는데,
사실 2차원 배열을 쓸 때도 역으로 순회해도 문제가 똑같이 풀린다.
2차원 배열을 쓰는 것은 이해의 편의를 직관적으로 돕기 위한 장치일 뿐이다.
이전까지의 최적 가치와 현재 물건을 넣어본 가치를
비교할 때 어느 위치에서 무슨 정보를 가져오는지,
왜 역으로 순회해야 중복이 방지되는지,
이 2가지를 이해하면 1차원 배열 풀이를 이해할 수 있을 것이다.
- 초기 상태:
dp배열은 모든 값이 0으로 초기화된다.dp[0]부터dp[K]까지 모든 값은 처음에 0이다.
- 역순 순회:
- 각 물품에 대해 배낭의 용량을 역순으로 순회한다.
- 역순으로 순회하기 때문에 현재 물품을 추가하기 전의 값들이 유지된다.
- 값 갱신:
dp[j] = max(dp[j], dp[j - weight] + value)식을 사용하여 값을 갱신한다.dp[j - weight]는 이미 이전 물품들을 고려하여 계산된 값입니다. 따라서dp[j - weight] + value는 현재 물품을 포함한 최대 값을 의미한다.
입력이 다음과 같을 때:
4 10
1 1
4 8
3 6
5 12
초기 dp 배열: [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
- 첫 번째 물품 (무게 1, 가치 1)을 처리:
dp배열을 역순으로 갱신:dp[10] = max(dp[10], dp[10-1] + 1) = max(0, 0 + 1) = 1dp[9] = max(dp[9], dp[9-1] + 1) = max(0, 0 + 1) = 1- ...
dp[1] = max(dp[1], dp[1-1] + 1) = max(0, 0 + 1) = 1- 결과:
[0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
- 두 번째 물품 (무게 4, 가치 8)을 처리:
dp[10] = max(dp[10], dp[10-4] + 8) = max(1, 1 + 8) = 9dp[9] = max(dp[9], dp[9-4] + 8) = max(1, 1 + 8) = 9- ...
dp[4] = max(dp[4], dp[4-4] + 8) = max(1, 0 + 8) = 8- 결과:
[0, 1, 1, 1, 8, 9, 9, 9, 9, 9, 9]
- 세 번째 물품 (무게 3, 가치 6)을 처리:
dp[10] = max(dp[10], dp[10-3] + 6) = max(9, 9 + 6) = 15dp[9] = max(dp[9], dp[9-3] + 6) = max(9, 9 + 6) = 15- ...
dp[3] = max(dp[3], dp[3-3] + 6) = max(1, 0 + 6) = 6- 결과:
[0, 1, 1, 6, 8, 9, 9, 14, 15, 15, 15]
- 네 번째 물품 (무게 5, 가치 12)을 처리:
dp[10] = max(dp[10], dp[10-5] + 12) = max(15, 9 + 12) = 21dp[9] = max(dp[9], dp[9-5] + 12) = max(15, 8 + 12) = 20- ...
dp[5] = max(dp[5], dp[5-5] + 12) = max(9, 0 + 12) = 12- 결과:
[0, 1, 1, 6, 8, 12, 13, 14, 15, 20, 21]
결과적으로, 최대 용량 10에서 얻을 수 있는 최대 가치는 21이다.
따라서, 역순으로 순회하고 dp[j]를 갱신하는 방식은 물품이 중복 사용되지 않도록 하면서 올바른 최적 값을 계산할 수 있다.
'📝 Study Notes > Algorithm' 카테고리의 다른 글
| Red-Black Tree (0) | 2024.08.02 |
|---|---|
| 플로이드 와샬 알고리즘 (Python) (0) | 2024.07.23 |
| LCS (Longest Common Sequence) 알고리즘 (0) | 2024.07.23 |
| 그래프, DFS, BFS (Python) (0) | 2024.07.23 |
| 트리 구조 (0) | 2024.07.23 |