📝 Study Notes/Algorithm
그래프, DFS, BFS (Python)
lazyArtisan
2024. 7. 23. 23:26
그래프
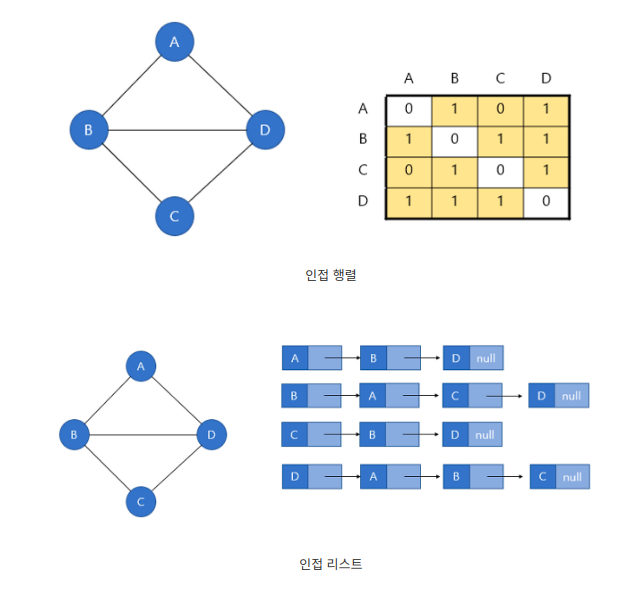
이미지 출처 : https://elisha0103.tistory.com/24
프로그래밍에서 그래프는 인접행렬, 인접리스트 방식으로 표현된다.
인접행렬: 2차원 배열로 그래프의 연결 관계를 표현하는 방식
- 메모리를 더 많이 쓰는 대신, 두 정점이 연결되었는지 확인하는 속도가 빠르다.
인접리스트: 리스트로 그래프의 연결 관계를 표현하는 방식
- 메모리를 덜 쓰는 대신에 두 정점의 연결 여부를 확인하는 데 시간이 걸린다.
간선의 개수가 많다면 인접 행렬이 유리하고, 간선의 개수가 적다면 인접 리스트가 유리하다.
그래프의 종류
- 무방향 그래프(Undirected Graph):
- 정점 간의 연결이 방향성을 가지지 않는 그래프입
- 방향 그래프(Directed Graph):
- 정점 간의 연결이 방향성을 가지는 그래프
- 가중치 그래프(Weighted Graph):
- 각 간선에 가중치(Weight)가 부여된 그래프
그래프의 표현 방식
1. 인접 행렬(Adjacency Matrix):
- 행렬의 각 요소 (i, j)는 정점 i에서 정점 j로의 간선이 있는지 여부를 나타낸다.
간선이 있으면 1(또는 가중치 값), 없으면 0으로 표시한다. - 장점: 두 정점 간의 간선 존재 여부를 O(1) 시간에 확인할 수 있다.
- 단점: 메모리 사용량이 많으며, 간선 수가 적은 희소 그래프(Sparse Graph)에서는 비효율적이다.
A B C
A 0 1 0
B 1 0 1
C 0 1 0
2. 인접 리스트(Adjacency List):
- 각 정점에 대해 해당 정점과 연결된 모든 정점을 리스트로 저장한다.
- 장점: 메모리 사용량이 적으며, 간선이 적은 그래프에서 효율적이다.
- 단점: 두 정점 간의 간선 존재 여부를 확인하는 데 O(n)의 시간이 걸릴 수 있다.
A: B
B: A, C
C: B
깊이 우선 탐색(DFS)
아래 레벨에 방문 안 한 노드가 있으면 그 노드를 우선 탐색
한 놈만 팬다
- 특정 경로가 존재하는지, 또는 모든 경로를 찾는 문제에 유용
- 그래프에서 사이클이 있는지 검사할 수 있다
- 재귀나 스택으로 구현한다
- 결과 하나를 만들어낸 뒤 다음 결과를 만들러 가기 때문에 검증하기가 쉽다
넓이 우선 탐색(BFS)
레벨별로 탐색한다
여러 놈을 한 대씩 때리며 간다
- 무방향 그래프에서 시작 정점에서 다른 정점까지의 최단 경로 찾을 수 있음
- 큐나 링크드 리스트를 사용한다
- DFS에 비해 경로 운빨을 덜 탄다 (시간 복잡도가 낮다)
BFS (Breadth-First Search) 구현
from collections import deque
def bfs(graph, start):
visited = set() # 방문한 노드를 기록할 집합
queue = deque([start]) # 시작 노드를 큐에 삽입
visited.add(start)
while queue:
vertex = queue.popleft() # 큐에서 노드를 하나 꺼냄
print(vertex, end=" ") # 방문한 노드를 출력
for neighbor in graph[vertex]:
if neighbor not in visited:
queue.append(neighbor) # 인접한 노드를 큐에 삽입
visited.add(neighbor) # 방문한 노드로 표시
# 그래프 예제 (인접 리스트)
graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
}
# BFS 실행
print("BFS:")
bfs(graph, 'A')DFS (Depth-First Search) 구현 - 재귀 방식
def dfs_recursive(graph, start, visited=None):
if visited is None:
visited = set()
visited.add(start)
print(start, end=" ") # 방문한 노드를 출력
for neighbor in graph[start]:
if neighbor not in visited:
dfs_recursive(graph, neighbor, visited)
# DFS 실행 (재귀 방식)
print("\nDFS (Recursive):")
dfs_recursive(graph, 'A')DFS (Depth-First Search) 구현 - 스택 사용
def dfs_stack(graph, start):
visited = set() # 방문한 노드를 기록할 집합
stack = [start] # 시작 노드를 스택에 삽입
while stack:
vertex = stack.pop() # 스택에서 노드를 하나 꺼냄
if vertex not in visited:
print(vertex, end=" ") # 방문한 노드를 출력
visited.add(vertex)
for neighbor in graph[vertex]:
if neighbor not in visited:
stack.append(neighbor) # 인접한 노드를 스택에 삽입
# DFS 실행 (스택 사용)
print("\nDFS (Stack):")
dfs_stack(graph, 'A')